Answer:
The correct option is D.
Explanation:
Let L be the number of latex balloons and M be the number of mylar balloon, M.
It is given that 17-inch latex balloons that require 2 cubic feet (ft^3) of helium and 18-inch mylar balloons that require only 0.5 ft^3.
Total amount of helium is
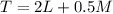
She only has access to 1,000 ft^3 of helium, 15% of which will be unused due to pressure loss in the tanks.
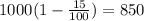
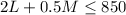
Therefore the
It is given that Joelle wants to have at least 500 balloons for sale in total.
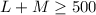
The system of inequalities is
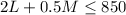
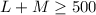
Therefore the correct option is D.