Question

Find the standard form of the equation of the parabola with a focus at (0, 8) and a directrix at y = -8

Answer 1

First, let
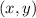
`(x,y)` be a point in our parabola. Since we know that the focus of our parabola is the point (0,8), we are going to use the distance formula to find the distance between the two points:

`\sqrt{(x-0)^(2)+(y-8)^(2)}`

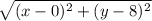
Next, we are going to find the distance between the directrix and the point in our parabola. Remember that the distance between a point (x,y) of a parabola and its directrix,
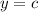
`y=c`, is:
`|y-c|`. Since our directrix is y=-8, the distance to our point will be:

`|y-(-8)|`

`|y+8|`

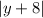
Now, we are going to equate those two distances, and square them to get rid of the square root and the absolute value:

`\sqrt{(x-0)^(2)+(y-8)^(2)}=|y+8|`

`(\sqrt{(x-0)^(2)+(y-8)^(2)})^(2)=|y+8|^(2)`

`(x-0)^(2)+(y-8)^(2)=y+8`

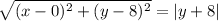
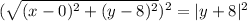
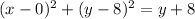
Finally, we can expand and solve for
`y`:

`x^2+y^2-16y+64=y^2+16y+64`

`x^(2)-16y=16y`

`32y=x^(2)`

`y= (1)/(32) x^2`

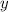
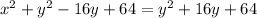
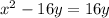
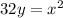
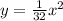
We can conclude that the standard form of the equation of the parabola with a focus at (0, 8) and a directrix at y = -8 is
`y= (1)/(32) x^(2)`