Which theorem or postulate proves that △ABC and △DEF are similar? Drag and drop the correct postulate or theorem into the box to correctly complete the statement.

Question

asked Feb 25, 2019 166k views

2 Answers

Radouane ROUFID · Answer 1 · 2019-03-03T02:35:11+0000

Answer: SSS similarity theorem

Explanation:

In the given figure we have two triangles ΔABC and ΔDEF.

Since we have given only the side lengths of the triangle.

Thus when we find the ratio of the corresponding sides we get,

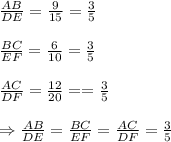
$(AB)/(DE)=(9)/(15)=(3)/(5)\\\\(BC)/(EF)=(6)/(10)=(3)/(5)\\\\(AC)/(DF)=(12)/(20)==(3)/(5)\\\\\Rightarrow(AB)/(DE)=(BC)/(EF)=(AC)/(DF)=(3)/(5)$

So by SSS similarity theorem, we have

ΔABC is similar to ΔDEF.

SSS similarity theorem says that if the lengths of the corresponding sides of two triangles are proportional then the triangles are similar triangles.