Question

Please explain how to solve this problem.

"The two triangles are similar. What is the value of x?"

Answer 1

The value of x is 5.

Explanation:

It is given that both triangles are similar.

In triangle ABC and DEC,

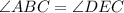`\angle ABC=\angle DEC` (Given)

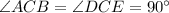`\angle ACB=\angle DCE=90^(\circ)` (Given)

By AA rule of similarity,

`\triangle ABC\sim \triangle DEC`

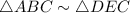
The corresponding sides of similar triangles are proportional.

`(AB)/(DE)=(BC)/(EC)=(AC)/(DC)`

`(4x)/(3x+1)=(3+12)/(12)`

`12* 4x=15* (3x+1)`

`48x=45x+15`

`3x=15`

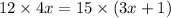
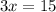
Divide both sides by 3.

`x=5`

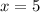
Therefore the value of x is 5.

Answer 2

Set up the proportion. That's what similar gives you the right to do.

(12 + 3) / 4x = 12 / (3x + 1) Cross multiply
15 * (3x + 1) = 12 * 4x Remove the brackets
45x + 15 = 48x Subtract 45x from both sides.
15 = 48x - 45x
15 = 3x
x = 5