Question

What length is the shorter leg of a right triangle that has hypotenuse 50 in long and its perimeter is 112 inches?

Answer 1

14

Explanation:

Pythagorean triple: {7, 24, 25}

Hypotenuse = 50

50 = 25*2

So, the two other legs are 7*2 = 14 and 24*2 = 48

We can confirm this by adding 14 + 48 + 50 = 112

Answer 2

The length of the shorter leg is 14 inches.

We will set up two equations for this; first, for the perimeter. We will call the legs a and b:

a + b + 50 = 112

Subtract 50 from both sides:
a + b + 50 - 50 = 112 - 50
a + b = 62

We will isolate a, so we can use substitution. Subtract b from both sides:
a + b - b = 62 - b
a = 62 - b

Now we will set up our Pythagorean theorem equation:
a² + b² = 50²
a² + b² = 2500

We will substitute our value for a from the first equation into this one:
(62-b)² + b² = 2500
(62 - b)(62 - b) + b² = 2500

Multiplying the binomials, we have:
62*62 - b*62 - b*62 -b(-b) + b² = 2500
3844 - 62b - 62b + b² + b² = 2500

Combining like terms:
3844 - 124b + 2b² = 2500

To set it equal to 0 and solve, we subtract 2500 from both sides:
3844 - 124b + 2b² - 2500 = 2500 - 2500
1344 - 124b + 2b² = 0

In standard form, we have
2b² - 124b + 1344 = 0

Using the quadratic formula,

`(--124\pm √((-124)^2-4(2)(1344)))/(2(2)) \\ \\=(124\pm √(15376-10752))/(4) \\ \\=(124\pm √(4624))/(4)=(124\pm 68)/(4)=(124+68)/(4)\text{ or }(124-68)/(4) \\ \\=(192)/(4)\text{ or }(56)/(4)=48\text{ or }14`

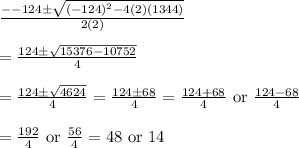
The shorter leg is 14 and the longer one is 48.