Question

A rectangular metal tank with an open top is to hold 171.5 cubic feet of liquid. what are the dimensions of the tank that require the least material to build?

Answer 1

To minimize the material usage we have to have the volume requested with the minimum surface area.
The volume is:

`171.5 =xyz`
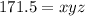
And the surface is:

`S=xy+2xz+2yz`
From the first equation we get:

`z=(171.5)/(xy) ; k=171.5\\ z=(k)/(xy)\\`
I will use k instead of a number just for the conveince.
We plug this into the second equation and we get:

`S=xy+2k(1)/(x)+2k(1)/(y)`
To find the minimum of this function we have to find the zeros of its first derivative.
Sx will denote the first derivative with respect to x and Sy will denote the first derivative with respect to Sy.

`S_x=y-2k(1)/(x^2)\\ S_y=x-2k(1)/(y^2)`
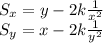
Now let both derivatives go to zero and solve the system (this will give us the so-called critical points).

`0=y-2k(1)/(x^2)\\ 0=x-2k(1)/(y^2)\\ y=2k(1)/(x^2)\\ x=2k(1)/(y^2)\\`
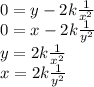
Now we plug in the first equation into the other and we get:

`x=((2k)/(1))/((4k^2)/(x^4))\\ x^3=2k\\ x=(2\cdot171.5)^(1/3)\\ x=7`
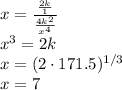
Now we can calculate y:

`y=2k(1)/(x^2)\\ y=2\cdot 171.5(1)/(7^2)=7`
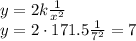
And finaly we calculate z:

`z=(171.5)/(xy)\\ z=(171.5)/(7\cdot7)=3.5`
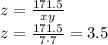
And finaly let's check our result:

`V=xyz=7\cdot7\cdot3.5=171.5`