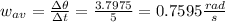Question

A child is pushing a merry-go-round. the angle through which the merry-go-round has turned varies with time according to θ(t)=γt+βt3, where γ= 0.422 rad/s and β= 1.35×10−2 rad/s3.

Answer 1

I attached the missing part of the question.
Part A
Angular velocity is simply the rate at which angle changes, in other words, it is the first derivative of the angle function with respect to time:

`\theta (t)=\gamma t+\beta t^3\\ w(t)=(d\theta(t))/(dt)\\ w(t)=\gamma +3\beta t^2`
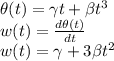Part B
Initial value is the value at t=0. To find initial value we simply plug t=0 into the equation.

`w(0)=\gamma +3\beta\cdot 0^2\\ w(0)=\gamma\\ w_0=\gamma= 0.422(rad)/(s)`
Part C
To find these values we simply need to plug in t=5 in the equation.

`w(5)=\gamma +3\beta\cdot 5^2\\ w(5)=\gamma +75\cdot \beta=0.422+75 \cdot 1.35\cdot10^(-2)=1.43(rad)/(s)`
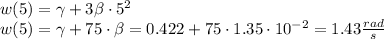Part D
Average angular velocity is total angular displacement divided by time:

`w_(av)=(\Delta \theta)/(\Delta t)`

`\Delta \theta=\theta(5)-\theta(0)=\gamma\cdot5+\beta 5^3\\ \Delta \theta=0.422\cdot5+125\cdot1.35\cdot10^(-2)=3.7975 $rad`
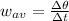
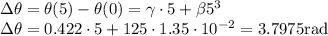
The average angular velocity is:

`w_(av)=(\Delta \theta)/(\Delta t)=(3.7975 )/(5)=0.7595(rad)/(s)`