Question

The volume of two similar figures are 512 mm3 and 3375 mm3. If the surface area of the smaller figure is 128mm2, what is the surface area of the larger figure?

__mm2
PLEASE HELP

Answer 1

The answer is 450 mm²

.........................................

Answer 2

--------------------------------------------------------
Find the ratio of thel length
--------------------------------------------------------

`((L_1)/(L_2))^3 = (V_1)/(V_2)`

--------------------------------------------------------
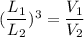
Substitute the value of the given volume
--------------------------------------------------------

`((L_1)/(L_2))^3 = ((512)/(3375) )`

--------------------------------------------------------
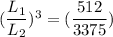
Cube Root both sides
--------------------------------------------------------

`((L_1)/(L_2)) = \sqrt[3]{(512)/(3375) }`

--------------------------------------------------------
Ratio of the length of the 2 similar rectangle
--------------------------------------------------------

`((L_1)/(L_2)) = (8)/(15)`

-----------------------------------------
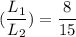
Find the area of the larger figure
-----------------------------------------

`((L_1)/(L_2))^2 = (A_1)/(A_2)`

--------------------------------------------------------
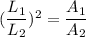
Substitute the known number to the ratio
--------------------------------------------------------

`((8)/(15))^2 = (128)/(A_2)`

--------------------------------------------------------
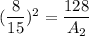
Evaluate the left hand side
--------------------------------------------------------

`(64)/(225) = (128)/(A_2)`

--------------------------------------------------------
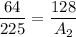
Cross multiply and Solve
--------------------------------------------------------

`64 * A_2=128 * 225`


`A_2 = 28800 / 64`


`A_2 = 450 \ mm^2`

--------------------------------------------------------
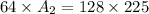
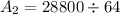
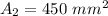
Answer: Area = 450 mm²
--------------------------------------------------------