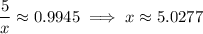Question

Out of 2,000 random but normally distributed numbers with a mean of 45 and a standard deviation of x, approximately 1,360 numbers are found to be between 40 and 50. What is the value of x?

Answer 1

Let
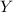
`Y` denote the random variable representing a given number in the total set of numbers. We're told that
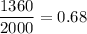
`(1360)/(2000)=0.68` of the numbers fall within a given range, so we know


`\mathbb P(40\le Y\le50)=0.68`

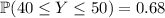
where
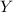
`Y` is normally distributed with mean 45 and an unknown variance
`x^2`.

Let's make the transformation to a random variable with a standard normal distribution:


`\mathbb P\left(\frac{40-45}x\le\frac{Y-45}x\le\frac{50-45}x\right)=\mathbb P\left(-\frac5x\le Z\le\frac5x\right)`

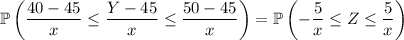
Since
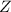
`Z` is symmetric, we have


`\mathbb P(-\frac5x\le Z\le\frac5x\right)=2\mathbb P\left(0\le Z\le\frac5x\right)=2\bigg(\mathbb P\left(Z\le\frac5x\right)-\mathbb P(Z\le0)\bigg)`

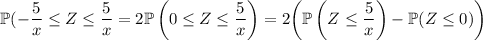
The mean of
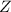
`Z` is 0, and by symmetry we know that exactly half of the distribution falls to the left of
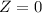
`Z=0`, so
`\mathbb P(Z\le0)=0.5`. We're left with


`0.68=2\mathbb P\left(Z\le\frac5x\right)-2\cdot0.5`

`\implies\mathbb P\left(Z\le\frac5x\right)=0.84`

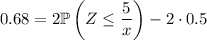
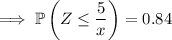
This probability corresponds to a value of
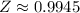
`Z\approx0.9945`, which means


`\frac5x\approx0.9945\implies x\approx5.0277`