Question

Find the are of a parallelogram that has a base of 7 1/2 and a height of 5 2/7

Answer 1

Use the formula for the area of a parallelogram:


`\sf A=bh`

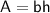
Plug in what we know:


`\sf A=(7(1)/(2))(5(2)/(7))`

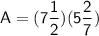
Convert both of them into improper fractions. We do this by multiplying the denominator to the whole number, adding it to the numerator, which becomes our new numerator, and we keep the denominator the same:


`\sf A=((15)/(2))((37)/(7))`

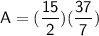
Now multiply the numerators and denominators together:


`\sf A=(15)/(2)\cdot(37)/(7)\rightarrow(15\cdot 37)/(2\cdot 7)\rightarrow(555)/(14)`

Convert it back into a mixed number. 14 goes into 555 thirty-nine times. 14 * 39 = 546. 555 - 546 = 9. So we have 39 wholes and 9 left over, or:


`\sf 39(9)/(14)`

So this is the area of the parallelogram.