Question

Arnold's company reimburses his expenses on food, lodging, and conveyance during business trips. The company pays $40 a day for food and lodging and $0.50 for each mile traveled. Arnold drove 400 miles and was reimbursed $2600. Part A: Create an equation that will determine the number of days x on the trip (3 points) Part B: Solve this equation justifying each step with an algebraic property of equality. (6 points) Part C: How many days did Arnold spend on this trip? (1 points)

Answer 1

We know for the problem that Arnold drove 400 miles during his business trip, and the cost of each mile is $0.50, so the total cost of the miles the company will reimburse is:
`(400)(0.5)=200`$.

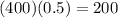
Part A. We now know that the total cost of the miles the company have to pay to Arnold is $200. We also know the company pays him $40 a day for food and lodging. So let
`x` represent the number of days of Arnold's business trip:

`y=40x+200`
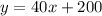
where

`y` is the amount the company will reimburse Arnold after
`x` days.

`x` is the number of days.

Part B. We know that the amount the company will reimburse Arnold is $2600, so
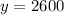
`y=2600`. Lets replace that value in our equation and solve for
`x` to find the number of days:

`y=40x+200`

`2600=40x+200`
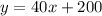
The first thing we are going to do to solve our equation is subtract 200 to both sides using the subtraction property of equality:

`2600-200=40x+200-200`

`2400=40x`
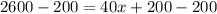
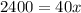
Next, we are going to divide both sides of the equation by 40, using the division property of equality, to find the value of
`x`:

`(2400)/(40) = (40x)/(40)`

`60=x`
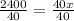
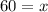
Finally, we can use the reflexive property of equality to get:

`x=60`

Part C. We can conclude that Arnold spend 60 days in his business trip.