Question

The data represents the heights of fourteen basketball players, in inches.

69, 70, 72, 72, 74, 74, 74, 75, 76, 76, 76, 77, 77, 82

If the highest and lowest numbers were dropped to form a new set of data how would the interquartile range of the new set compare to the interquartile range of the original set?

The interquartile range of the new set would be the interquartile range of the original set.

Answer 1

Interquartile range of the old set = 76 - 72 = 4
Interquartile range of the new set = 76 - 73 = 3

IQR of new est < old set.

Answer 2

The interquartile range of the new set is less than the interquartile range of the original set.

Explanation:

Given : 69, 70, 72, 72, 74, 74, 74, 75, 76, 76, 76, 77, 77, 82

To Find : If the highest and lowest numbers were dropped to form a new set of data how would the inter quartile range of the new set compare to the inter quartile range of the original set?

Solution:

Data : 69, 70, 72, 72, 74, 74, 74, 75, 76, 76, 76, 77, 77, 82

No. of terms = 14

Median =
`\frac{(n)/(2)\text{th term}+((n)/(2)+1)\text{th term}}{2}`

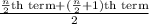
Median =
`\frac{(14)/(2)\text{th term}+((14)/(2)+1)\text{th term}}{2}`

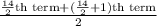
Median =
`\frac{7\text{th term}+(8)\text{th term}}{2}`

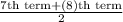
Median =
`(74+75)/(2)`

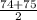
Median =
`74.5`

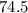
`Q_1` is the median of the lower half of data ( data below the median)

Data : 69, 70, 72, 72, 74, 74, 74

No. of terms = 7

Median = 4th term =72

`Q_1=72`

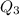`Q_3` is the median of the upper half of data ( data above the median)

Data : 75, 76, 76, 76, 77, 77, 82

No. of terms = 7

Median = 4th term =76

`Q_3=76`

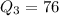
IQR =
`Q_3-Q_1=76-72=4`

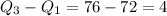
Now the highest and lowest numbers were dropped to form a new set of data

So, new data : 70, 72, 72, 74, 74, 74, 75, 76, 76, 76, 77, 77

No. of terms = 12

Median =
`\frac{(n)/(2)\text{th term}+((n)/(2)+1)\text{th term}}{2}`

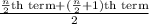
Median =
`\frac{(12)/(2)\text{th term}+((12)/(2)+1)\text{th term}}{2}`

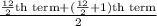
Median =
`\frac{6\text{th term}+(7)\text{th term}}{2}`

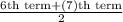
Median =
`(74+75)/(2)`

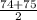
Median =
`74.5`

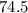
`Q_1` is the median of the lower half of data ( data below the median)

Data: 70, 72, 72, 74, 74, 74,

No. of terms = 6

Median =
`\frac{3\text{rd term }+4 \text{th term}}{2}`

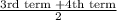
Median =
`(72+74)/(2)=73`

`Q_1=73`

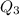`Q_3` is the median of the upper half of data ( data above the median)

Data : 75, 76, 76, 76, 77, 77

No. of terms = 6

Median =
`\frac{3\text{rd term }+4 \text{th term}}{2}`

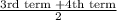
Median =
`(76+76)/(2)=76`

`Q_3=76`

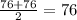
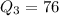
IQR =
`Q_3-Q_1=76-73=3`

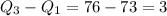
Thus IQR of old data set is greater than IQR of new data set i.e. 4>3

Hence The interquartile range of the new set is less than the interquartile range of the original set.