Question

What is the expression in radical form? (7x^3y^2) 2/7

Answer 1

`\sqrt[7]{(7x^3y^2)^(2) } = \sqrt[7]{(49x^6y^4)}`
In a fractional exponent the denominator tells what root it is (7th root in this case) and the numerator tells what the value in the parenthesis is raised to (2nd power in this case)

Answer 2

`\sqrt[7]{49x^6y^4}`

Explanation:

`(7x^3y^2) ^{(2)/(7) }`

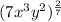
Apply exponential property to get radical form

To get radical form we look at the fraction in the exponent

The numerator 2 gets multiplied with the exponents inside the radical and denominator 7 goes into the radical outside

`a^(m)/(n)=\sqrt[n]{a^m}`

`(7x^3y^2)^{(2)/(7)}`

`\sqrt[7]{(7x^3y^2)^2}`

Multiply exponent 2 inside the parenthesis

`\sqrt[7]{(7^2x^6y^4)}`

`\sqrt[7]{49x^6y^4}`