Question

The given line segment has a midpoint at (−1, −2).

What is the equation, in slope-intercept form, of the perpendicular bisector of the given line segment?

y = −4x − 4
y = −4x − 6
y = x – 4
y = x – 6

Answer 1

y = -4x - 6. This is the only option that goes through the given point. 

Answer 2

Option 2 is correct. y=-4x-6

Explanation:

We are given a point (-1,-2). This is mid point of given segement.

Let AB be asegement with mid point M(-1,-2) as shown in figure.

We need to find the equation line in slope intercept form which is perpendicular bisector of segement AB.

As we know perpendicular bisector line always passing through the mid point of segement.

So, we will check given point (-1,-2) with all option to satisfy.

Option 1) y=-4x-4

Put x=-1 and y=-2 into equation and we get

`-2=-4(-1)-4`

`-2\\eq 0`

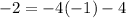
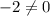
Does't satisfy this equation. This won't be a solution.

Option 2) y=-4x-6

Put x=-1 and y=-2 into equation and we get

`-2=-4(-1)-6`

`-2=-2`

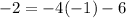
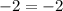
(-1,-2) satisfy given equation y=-4x-6. This would be solution.

Option 3) y=x-4

Put x=-1 and y=-2 into equation and we get

`-2=-1-4`

`-2\\eq -5`

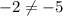
Does't satisfy this equation. This won't be a solution.

Option 4) y=x-6

Put x=-1 and y=-2 into equation and we get

`-2=-1-6`

`-2\\eq -7`

Does't satisfy this equation. This won't be a solution.