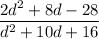Question

Simplify the sum. d^2-9d+20/d^2-3d-10 plus d^2-2d-8/d^2+4d-32

Answer 1

For this case what you should do is follow the following steps:
1) factorize numerator and denominator of both expressions.
2) cancel similar terms
3) add both fractions by cross product
4) Rewrite the numerator and denominator.
Answer:
See attached image.

Answer 2

Hence, the final result after simplification is:

`(2d^2+8d-28)/(d^2+10d+16)`

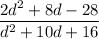
Explanation:

We have to simplify the sum:

d^2-9d+20/d^2-3d-10 plus d^2-2d-8/d^2+4d-32 i.e.

`(d^2-9d+20)/(d^2-3d-10)+(d^2-2d-8)/(d^2+4d-32)`

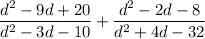
now we will apply the method of splitting the middle term in each of the polynomial terms in the numerator and denominator to obtain:

`=(d^2-5d-4d+20)/(d^2-5d+2d-10)+(d^2-4d+2d-8)/(d^2+8d-4d-32)\\\\\\\\=(d(d-5)-4(d-5))/(d(d-5)+2(d-5))+(d(d-4)+2(d-4))/(d(d+8)-4(d+8))\\\\\\=((d-4)(d-5))/((d+2)(d-5))+((d+2)(d-4))/((d+8)(d-4))\\\\\\=(d-4)/(d+2)+(d+2)/(d+8)\\\\\\=((d-4)(d+8)+(d+2)(d+2))/((d+2)(d+8))`

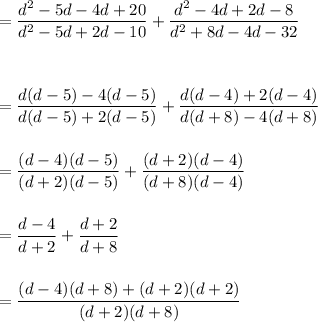
which on solving gives us the final result as:

`(2d^2+8d-28)/(d^2+10d+16)`