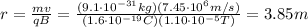Question

A cosmic ray electron moves at 7.45 â 106 m/s perpendicular to the earth's magnetic field at an altitude where field strength is 1.10 â 10â5 t. what is the radius (in m) of the circular path the electron follows?

Answer 1

The magnetic force on the electron is:

`F=qvB \sin \theta`
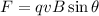
where q is the electron charge, v the electron speed, B the magnetic field intensity and
`\theta` is the angle between v and B. Since the electron is traveling perpendicular to the magnetic field,
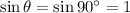
`\sin \theta = \sin 90^(\circ)=1`, so we can write

`F=qvB`

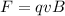
This force acts as centripetal force of the motion,
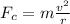
`F_c = m (v^2)/(r)`, where m is the electron mass and r the radius of the circular orbit. So we can write:

`qvB=m (v^2)/(r)`
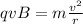
and by re-arranging this equation, we find the radius of the circular orbit, r:

`r= (mv)/(qB)= ((9.1 \cdot 10^(-31)kg)(7.45 \cdot 10^6 m/s))/((1.6 \cdot 10^(-19)C)(1.10 \cdot 10^(-5)T))= 3.85 m`