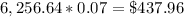Question

A field is to be fertilized at a cost of $0.07 per square yard. The rectangular part of the field is 125 yd long and the diameter of each semicircle is 40 yd. Find the cost of fertilizing the field.

Answer 1

The cost of fertilizing the field is
`\$437.96`

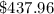
Explanation:

we know that

The area of the figure is equal to the area of the rectangle plus the area of a complete circle (two semicircles)

Step 1

Find the area of the rectangle

The area of rectangle is equal to

`A=LW`

where

L is the length side of rectangle

w is the width side of the rectangle

In this problem we have

`L=125\ yd`

`W=D=40\ yd`

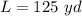
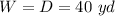
substitute

`A=125*40=5,000\ yd^(2)`

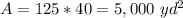
Step 2

Find the area of the circle

The area of the circle is equal to

`A=\pi r^(2)`

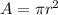
where

r is the radius of the circle

In this problem we have

`r=40/2=20\ yd`

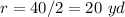
substitute

`A=\pi (20)^(2)=1,256.64\ yd^(2)`

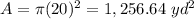
Step 3

Find the area of the figure

Adds the area of rectangle and the area of the circle

`5,000\ yd^(2)+1,256.64\ yd^(2)=6,256.64\ yd^(2)`

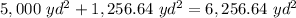
Step 4

Find the cost

Multiply the total area by
`0.07 (\$)/(yd^(2) )`

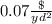
so

`6,256.64*0.07=\$437.96`