Question

What term has to be added to x^2-3x to be a trinomial 3/2 9/4 6 9

Answer 1

Answer: The correct option is (B)
`(9)/(4).`

Step-by-step explanation: We are given to find the term that has to be added to
`x^2-3x` to be a perfect trinomial.

Let, c denote the term to be added.

Then,

`x^2-3x+c\\\\=x^2-2* x* (3)/(2)+c\\\\\\=x^2-2* x* (3)/(2)+(9)/(4)+c-(9)/(4)\\\\\\=\left(x-(3)/(2)\right)+c-(9)/(4).`

Therefore, the given expression will be a perfect trinomial if

`c-(9)/(4)=0\\\\\\\Rightarrow c=(9)/(4).`

Thus, the required term to be added is
`(9)/(4).`

Option (B) is CORRECT,

Answer 2

Your question is probably what should be added to the given expression to make it a perfect square.

The given expression is:


`x^(2) -3x`

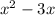
The formula of
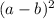
`(a-b)^(2)` is
`a^(2) -2ab+ b^(2)`

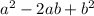
Re-writing the given expression:


`x^(2) - 2(x)( (3)/(2))`

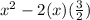
So, we have the square of first term and twice the product of first and second term. What is missing is the square of second term.

So, the complete expression for perfect square will be:


`x^(2) -2(x)( (3)/(2))+ ( (3)/(2) )^(2) \\ \\ x^(2) -2(x)( (3)/(2))+ (9)/(4)`

Therefore, 9/4 should be added to the given expression to make it a perfect square.