The firts thing we are going to do here is use the simple interest formula:
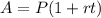
where

is the final amount after

years

is the initial investment

is the interest rate in decimal form

is the number of years
With this formula we will find the final amount Azhar's investment after 7 years. We know from our problem that
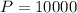
,
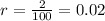
, and

. Lets replace those values in our formula to find

:
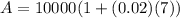
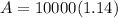
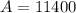
Now, since Sarah is investing in a compound interest account, we are going to use the compound interest formula:
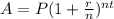
where

is the final amount after

years

is the initial investment

is the interest rate in decimal form

is the number of times the interest is compounded per year

is the number of years
Notice that we know from our problem that after 7 years their investments are worth the same amount, so
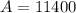
. We also know that
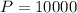
,
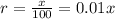
, and

. Since the interest are compounded per year,
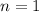
. Lets replace all the vales in our compound interest formula and solve for

to find our rate:
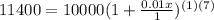
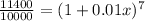
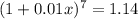
![1+0.01x= \sqrt[7]{1.14}](https://img.qammunity.org/2019/formulas/mathematics/high-school/qicojqctl7zcxinsh29sc5km6dzqhqy2ft.png)
![0.01x= \sqrt[7]{1.14} -1](https://img.qammunity.org/2019/formulas/mathematics/high-school/jww3jf5sntaqlft8ci6o4zb7nklkt44o4y.png)
![x= \frac{ \sqrt[7]{1.14}-1 }{0.01}](https://img.qammunity.org/2019/formulas/mathematics/high-school/wg0zefw6o7ex8oa3501j2b8exebvkm9izc.png)
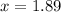
We can conclude that the interest rate of
Sarah's investment is approximately 1.89%, so x=1.89%.