Question

If the sin 60° = square root of three over two, then which statement is true? (6 points)

cos 30° = square root of three over two, because the cosine and sine are complements
cos 30° = 0, because the cosine and sine are complements
cos 120° = square root of three over two, because the cosine and sine are supplements
cos 120° = 0, because the cosine and sine are supplements

Answer 1

The first one, which states that cos(30 deg) are complements

Answer 2

Answer: The answer is (a) cos 30° = square root of three over two, because the cosine and sine are complements

Step-by-step explanation: Given that -

`\sin 60^\circ=(\sqrt 3)/(2).`

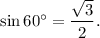
we are to select the correct statement from the given four options.

We know that sine and cosine functions are supplement of each other. So, we have

`\sin 60^\circ=\cos(90^\circ-60^\circ)=\cos 30^\circ=(\sqrt 3)/(2).`

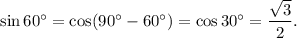
Thus, the correct option is (a) cos 30° = square root of three over two, because the cosine and sine are complements.