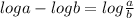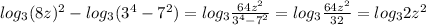Question

What is 2 (log₃8+log₃z) - log₃(3⁴-7²) written as a single logarithm?

Answer 1

Before we start solving this problem we need to make sure that all logarithms have same base. They do. Base is 3.

We start by solving first brackets. We will use the rule:

`log a + log b = log (a*b)`


`log_(3) 8 + log_(3) z = log_(3) (8z)`

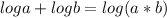
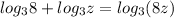
Now we are left with:

`2log_(3) (8z)- log_(3) ( 3^(4) - 7^(2) )`

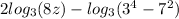
To get rid of 2 we will use rule:

`a* log_(b) c= log_(b) c^(a)`


`2log_(3) (8z)= log_(3) (8z)^(2)`

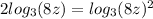
Now we are left with:

`log_(3) (8z)^(2)-log_(3) ( 3^(4) - 7^(2) )`

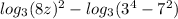
To solve this we will use rule:

`log a -logb = log (a)/(b)`


`log_(3) (8z)^(2)-log_(3) ( 3^(4) - 7^(2) )= log_(3) (64 z^(2) )/(3^(4) - 7^(2)) =log_(3) (64 z^(2) )/(32) =log_(3) 2z^(2)`