Question

The sun is 25 degrees above the horizon. find the length of a shadow cast by a building that is 100 feet tall. round your answer to two decimal places. the length of the shadow is ____ feet.

Answer 1

214.45 feet.

Explanation:

Please find the attachment.

Let x be the length of building's shadow.

We have been given that the sun is 25 degrees above the horizon. The length of the building is 100 feet tall.

We can see from our attachment that the length of the building is opposite side and the length of the shadow is adjacent side for the angle of 25 degrees.

Since tangent relates the opposite side of right triangle with adjacent side, so we can set an equation to find the length of building's shadow as:

`\text{tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

`\text{tan}(25^(\circ))=(100)/(x)`

`x=\frac{100}{\text{tan}(25^(\circ))}`

`x=(100)/(0.466307658155)`

`x=214.45069\approx 214.45`

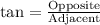
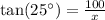
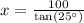
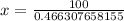
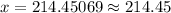
Therefore, the length of shadow cast by the building is 214.45 feet.

Answer 2

Answer
214.45 feet

Explanation
The sun is 250 above the horizon. This means that the angle of elevation is 25o.
Since you have been given the height of the building, you can use the trigonometric ratio (tangent) to find the length of the shadow (l).
tan⁡〖= 〗 oposite/adjacent
tan⁡25=100/l
l=100/tan⁡25 =214.4506921
Length of the shadow = 214.4506921 feet