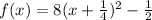Question

What is f(x)=8x2+4x written in vertex form

Answer 1

f(x)=8(x^2+1/2x)
using completing the square:
f(x)=8(x^2+1/2x+1/16)-(8*1/16) -->since we added a 1/16 inside the parenthesis, we need to subtract that quantity times 8
f(x)=8(x+1/4)-1/2

Answer 2

Vertex form:

`f(x)=8(x+(1)/(4))^2-(1)/(2)`

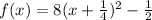
Explanation:

Given:
`f(x)=8x^2+4x`

We need to write in vertex form.

Vertex form:

`y=a(x-h)^2+k`

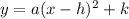
vertex: (h,k)

`f(x)=8x^2+4x`

Step 1: Take out 8 common from each term

`f(x)=8(x^2+(1)/(2)x)`

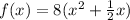
Step 2: Add and subtract square of half of coefficient of x

`f(x)=8(x^2+(1)/(2)x+(1)/(16)-(1)/(16))`

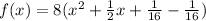
Step 3: Factor the term inside parentheses

`f(x)=8(x^2+2\cdot (1)/(4)\cdot x+((1)/(4))^2)-8\cdot (1)/(16))`

`f(x)=8(x+(1)/(4))^2-(1)/(2)`
`\because (a^2+2ab+b^2)=(a+b)^2`

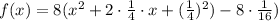
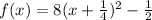
Hence, The vertex form of f(x)

`f(x)=8(x+(1)/(4))^2-(1)/(2)`