Question

Please Help!!!

(x-3)^2/64 + (y+5)^2/100 = 1

a. Identify the coordinates of the center of the ellipse.
b. Find the length of the major and minor axes.
c. Find the coordinates of the foci.
d. Graph the ellipse. Label the center and foci.,

Answer 1

Your ellipse is given in the form:

`((x - xc)^(2) )/( a^(2) ) + ((y - yc)^(2) )/( b^(2) ) = 1`

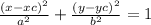
Indeed, you have:


`((x-3)^(2) )/(64) + ((y+5)^(2) )/(100) = 1`

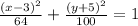
Therefore you can easily find:

a) the coordinates of the center:
in your case xc = 3 and yc = -5
hence C(3 , -5)

b) lenght of the major and minor axis:
in your case a² < b²:
a² = 64 ⇒ a = 8 (ATTENTION! This is the semi-minor axis)
b² = 100 ⇒ b = 10 (again, this is the semi-major axis)
Therefore,
minor axis 2a = 16 and major axis 2b = 20

c) coordinates of the foci:
Since you have a² < b², foci have the generic coordinates F₁₂ (xc , yc+/-c)
where c = √(b² - a²)

Let's compute c = √(100 - 64) = √36 = 6
yf₁ = -5 - 6 = -11
yf₂ = -5 + 6 = -1
Therefore:
F₁ (3, -11) and F₂(3, +1)

d) the graph is in the picture attached