Question

Suppose you have a spherical balloon filled with air at room temperature and 1.0 atm pressure; its radius is 17 cm. You take the balloon in an airplane, where the pressure is 0.87 atm. If the temperature is unchanged, what's the balloon's new radius?,

Answer 1

The new radius of the balloon is 17.8 cm.

Step-by-step explanation:

Initial pressure of the air in the balloon =
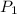`P_1` 1.0 atm

Radius of the balloon ,r= 17 cm

Volume of the spherical volume balloon =
`V_1=(4)/(3)\pi r^3`

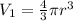
Final pressure of the air in balloon =
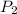`P_2`=0.87 atm

Radius of the balloon be R

Volume of the balloon be =
`V_2=(4)/(3)\pi R^3`

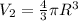
New radius of the balloon= R

According Boyle's Law:

`P_1V_1=P_2V_2`

`1.0 atm* (4)/(3)\pi r^3=0.87 atm* (4)/(3)\pi R^3`

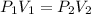
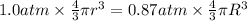
R =17.80 cm

The new radius of the balloon is 17.8 cm.

Answer 2

Answer: 17.8 cm


Step-by-step explanation:


1) Since temperature is constant, you use Boyle's law:


PV = constant => P₁V₁ = P₂V₂


=> V₁/V₂ = P₂/P₁

2) Since the ballon is spherical:


V = (4/3)π(r)³

Therefore, V₁/V₂ = (r₁)³ / (r₂)³


3) Replacing in the equation V₁/V₂ = P₂/P₁:


(r₁)³ / (r₂)³ = P₂/P₁

And you can solve for r₂: (r₂)³ = (P₁/P₂) x (r₁)³


(r₂)³ = (1.0 atm / 0.87 atm) x (17 cm)³ = 5,647.13 cm³

r₂ = 17.8 cm