Question

determine whether each set of side lengths could be the sides of a right triangle Drag and drop each set of side lengths to the correct box right triangle not a right triangle 8 in 15 in 17 in. 4 in 15 in 17 in

Answer 1

"8 in., 15 in., 17 in." is a right triangle and "4 in., 15 in., 17 in." is not a right triangle. Hope this helps!

Answer 2

8 in 15 in 17 in.--- form a right angled triangle.

4 in 15 in 17 in.---- do not form a right angled triangle.

Explanation:

We know that according to the PYTHAGOREAN THEOREM of right triangles we have:

`c^2=a^2+b^2`

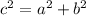
where c is the hypotenuse or the largest side of a triangle and a and b are other two legs of a right triangle,.

1)

8 in 15 in 17 in.

`17^2=15^2+8^2\\\\289=225+64\\\\289=289`

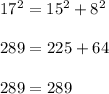
Hence, the given measure of sides form a side of a right angled triangle.

2)

4 in 15 in 17 in.

Since,

`17^2\\eq 15^2+4^2`

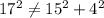
Hence, the given measure of sides do not form a side of a right angled triangle.