Question

Or an angle θ with the point (−20, −21) on its terminating side, what is the value of cosine?

Answer 1

The value of cosine is
`\cos \theta=-(20)/(29)`.

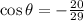Explanation:

It is given that an angle θ with the point (−20, −21) on its terminating side.

It means the right angle triangle is formed in third quadrant where length of the perpendicular is 21 and the base is 20.

According to the Pythagoras theorem,

`hypotenuse^2=base^2+perpendicular^2`

`hypotenuse^2=(20)^2+(21)^2`

`hypotenuse^2=400+441`

`hypotenuse^2=841`

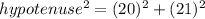
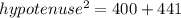
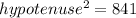
Taking square root both the sides.

`hypotenuse=√(841)`

`hypotenuse=29`

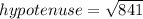
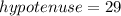
In a right angled triangle,

`\cos \theta=(base)/(hypotenuse)`

`\cos \theta=(20)/(29)`

θ lie in the third quadrant and cosine is negative in third quadrant.

`\cos \theta=-(20)/(29)`

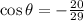
Therefore the value of cosine is
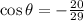`\cos \theta=-(20)/(29)`.

Answer 2

cos(θ) = -20/√((-20)^2 +(-21)^2)
.. = -20/-√841 . . . . . . . . . . . . . . . . . θ is a 4th-quadrant angle, so cos(θ) > 0
.. = 20/29

The value of the cosine is 20/29.