Question

A circle could be circumscribed abut the quadrilateral below

Answer 1

Hello,
False
since
m∠B + m∠D must be equal to 180°
and
m∠A + m∠C must be equal to 180°

Answer 2

B. False.

Explanation:

We have been given an image of a quadrilateral. We are asked to determine whether a circle could be circumscribed about the given quadrilateral.

We know that opposite angles of a cyclic quadrilateral are supplementary.

Let us check is this true for our given quadrilateral or not.

`m\angle B+m\angle D=180^(\circ)`

`80^(\circ)+60^(\circ)=180^(\circ)`

`140^(\circ)\\eq 180^(\circ)`

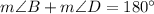
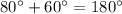
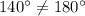
Now let us check other pair of angles.

`m\angle A+m\angle C=180^(\circ)`

`110^(\circ)+110^(\circ)=180^(\circ)`

`220^(\circ)\\eq 180^(\circ)`

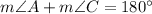
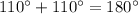
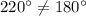
Since opposite angles of our given quadrilateral are not supplementary, therefore, a circle could not be circumscribed about the given quadrilateral.