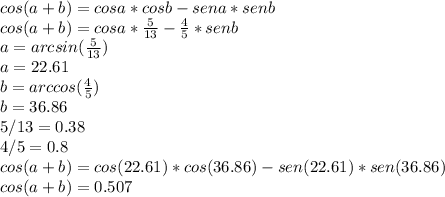Question

If a and b are two angles in standard position in Quadrant I, find cos(a+b) for the given function values. sin a=4/5 and cos b=5/13

Answer 1

cos(a+b)≈0.507

Explanation:

Hi there, in Quadrant I both sine and cosine functions are positive.

This cos (a+b) being a Classical Trigonometrical Identity, the product of the sum between two cosines equals the product of two cosines minus the product of two sines.

But we need to find the value of a and b, so that we can go on. Calculate the arccosine and arcsine function respectively is mandatory

`cos(a+b)=cosa*cosb-sena*senb\\ cos(a+b)=cosa*(5)/(13) -(4)/(5)*senb\\ a=arcsin((5)/(13))\\a=22.61\\b=arccos((4)/(5))\\b=36.86\\ 5/13=0.38\\4/5=0.8\\cos(a+b)=cos(22.61)*cos(36.86) -sen(22.61)*sen(36.86)\\ cos (a+b)=0.507`

Answer 2

First let's find the angles a and b.

We have then:
sin a = 4/5
a = Asin (4/5)
a = 53.13 degrees.

cos b = 5/13
b = Acos5 / 13
b = 67.38 degrees.

We now calculate cos (a + b). To do this, we replace the previously found values:
cos ((53.13) + (67.38)) = - 0.507688738
Answer:
-0.507688738
Note: there is another way to solve the problem using trigonometric identities.