Answer:
we can do it by simplifying 8 to
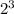 to make both powers base two, and subtracting the exponents.
to make both powers base two, and subtracting the exponents.
Explanation:
We have been given the expression
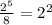
8 can be rewritten as
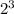
Hence, the given expression becomes
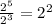
After subtracting the exponents on left hand side of the equation we get:

we can do it by simplifying 8 to
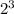 to make both powers base two, and subtracting the exponents.
to make both powers base two, and subtracting the exponents.