Question

2. Find x and y, given that line KL and line MN are parallel. Show all work

Answer 1

Did you get the answer?? I am on this test rn lol

Answer 2

`x=9.5`

`y=8.8`

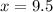
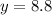
Explanation:

We have been given a diagram of triangles. We are asked to find the value of x and y.

We can see that triangle JKL and JMN share same vertex that is angle J. Since line KL is parallel to line MN, therefore, there corresponding angles will be equal.

Therefore, Angle-angle-angle similarity
`\Delta JKL\sim \Delta JMN`.

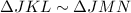Since corresponding sides of similar triangles are always proportional, so we can set a proportion for the sides of our given triangles as:

`(x-2)/(5)=(12)/(8)`

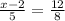
Upon cross multiplying our equation we will get,

`8(x-2)=12*5`

`8x-16=60`

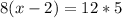
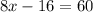
Let us add 16 to both sides of our equation.

`8x-16+16=60+16`

`8x=76`

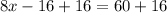
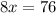
Let us divide both sides of our equation by 8.

`(8x)/(8)=(76)/(8)`

`x=9.5`

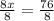
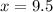
Therefore, x equals 9.5.

We can also set a proportion to solve for y as:

`(y)/(22)=(8)/(12+8)`

`(y)/(22)=(8)/(20)`

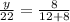
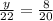
Upon cross multiplying our equation we will get,

`20y=22*8`

`20y=176`

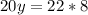
Let us divide both sides of our equation by 20.

`(20y)/(20)=(176)/(20)`

`y=8.8`

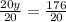
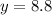
Therefore, y equals 8.8.