Question

Sammy is 5 feet 3 inches tall. He casts a shadow that is 31 feet 6 inches long. He is standing next to a stop sign that casts a shadow that is 40 feet 6 inches long. How tall is the stop sign in feet and inches.

Answer 1

Both Sammy and the stop sign form right angles with the ground. They also have the same angle of depression, where the sun hits them and casts their shadows. This means the third angle of each triangle must be congruent as well. Therefore the triangles will be similar. Since they are similar, we will use a proportion to solve this problem. First I convert the feet and inches to only inches. 5 ft 3 in = 63 in; 31 ft 6 in = 378 in; 40 ft 6 in = 486 in. The proportion will then be

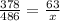
`(378)/(486)=(63)/(x)`. This comes because we compare corresponding sides of the similar triangles. 378 corresponds with 486, since they are the horizontal lengths of the shadows. 63 corresponds to x, since they are the heights of Sammy and the sign. Solving this by cross multiplication:

`378*x=63*486 \\378x=30618`
Divide both sides by 378:

`(378x)/(378)=(30618)/(378) \\x=81`
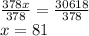
The sign is 81 inches tall. Converting this to feet and inches, divide by 12; this gives us 6.75. We have 6 feet and 0.75 feet. 0.75 feet * 12 inches per foot = 9 inches. The sign is 6 feet 9 inches tall.