Question

Three people become infected with a virus that spreads quickly. Each day that passes, the number of infected people doubles. How can the number of infected people be determined from the number of days that have passed?

Answer 1

`a_(n)=(2)^(n-1)`

Explanation:

The given problem models a geometric sequence, because each day is double than the day before.

So, if
`a_(1)` represents the first day,
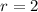`r=2` represents the increasing reason and
`a_(n)` represents the day
`n`, or the final day you can say.

Using all these elements, the sequence can be modelled as

`a_(n)=a_(1)r^(n-1)\\ a_(n)=1(2)^(n-1)\\a_(n)=(2)^(n-1)`

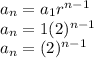
Where the first day is 1.

For example, after 20 days, that is,
`n = 20`, the number of infected people would be

`a_(n)=(2)^(n-1)\\a_(20)=(2)^(20-1)=(2)^(19)`

Therefore, the expression that models this problem is

`a_(n)=(2)^(n-1)`

Answer 2

`3x * 2 = y`
this is what I would come up with because.
y=the number of people infected
x=the number of days that have passed