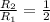Question

Wire 2 is twice the length and twice the diameter of wire 1. what is the ratio r2 / r1 of their resistances?

Answer 1

We can begin with the following formula for the resistance of a wire:

`R= \rho (L)/(A)`
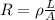
We assume that resistivity
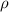
`\rho` of both wires is the same. So they differ in length
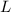
`L` and cross-sectional area
`A`.
We assume that both wires are perfect cylinders, which means that their cross section is given by the following formula:

`A= \pi r^(2)`.
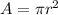
Where r is the radius of a wire. Diameter is just 2*r.
With all of this information, we can write equations for the resistance of both wires and then just divide them to find the ratio.
For wire 2 we have:

`R_(2) =\rho (2L)/(4 \pi r^(2) )`
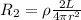
For cross section A, we write
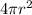
`4 \pi r^(2)`, because if the diameter of wire two is twice as big that means it's radius is twice as big. Keep in mind we are only interested in ratios here.
For wire 1 we write:

`R_(1)=\rho (L)/( r^(2) \pi )`.
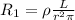
When we divide those two equations we get:

`( R_(2) )/( R_(1) )= (1)/(2)`