Question

Enos took out a 25-year loan for $135,000 at an APR of 6.0%, compounded monthly, and he is making monthly payments of $869.81. What will his balance be with 16 years left on the loan?

A.$107,193.28
B.$72,449.19
C.$131,763.43
D.$133,211.26

Answer 1

$107,193.28

Explanation:

Answer 2

Present value = 135000
Monthly interest, i = 0.06/12 = 0.005
Monthly payment, A= 869.81

Future value of loan after 16 years

`F=P(1+i)^n` [compound interest formula]

`=135000(1+.005)^(16*12)`

`=351736.652`

Future value of payments after 16 years

`(A((1+i)^n-1))/(i)`

`=(869.81((1+0.005)^(16*12)-1))/(0.005)`

`=279287.456`

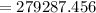
Balance = future value of loan - future value of payments
=351736.652-279288.456
= $ 72448.20

Note: the exact monthly payment for a 25-year mortgage is

`A=(P(i*(1+i)^n))/((1+i)^n-1)`

`=(135000(0.005*(1+0.005)^(25*12))/((1+0.005)^(25*12)-1)`

`=869.806892`

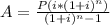
Repeating the previous calculation with this "exact" monthly payment gives
Balance = 72448.197, very close to one of the choices.

So we conclude that the exact value obtained above differs from the answer choices is due to the precision (or lack of it) of the provided data.

The closest choice is therefore $72,449.19