Question

Two students form a group of eight boys and 12 girls are sent to represent the school in a parade. If the two students are chosen at random, what is the probability that the students chosen are not both girls?

Answer 1

your best option would be 33/95 hope this helps

Answer 2

Answer: The required probability is 65.26%.

Step-by-step explanation: Given that two students form a group of eight boys and 12 girls are sent to represent the school in a parade.

We are to find the probability that the students chosen are not both girls, if the two students are chosen at random.

Total number of students in the group = 8 + 12 = 20.

Let S denote the sample space for the experiment of selecting two students and A denote the event that both the students are not girls.

Then,

`n(S)\\\\=^(20)C_2\\\\\\=(20!)/(2!(20-2)!)\\\\\\=(20*19*18!)/(2*1*18!)\\\\=190,\\\\\\\\n(A)\\\\\\=^8C_2*^(12)C_0+^8C_1*^(12)C_1\\\\\\=(8!)/(2!(8-2)!)*1+8*12\\\\\\=28+96\\\\=124.`

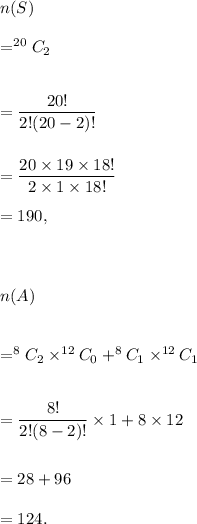
Therefore, the probability of event A is given by

`P(A)=(n(A))/(n(S))=(124)/(190)=(62)/(95)*100\%=65.26\%.`

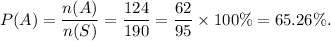
Thus, the required probability is 65.26%.