Question

What is the perimeter of the trapezoid with vertices Q(8, 8), R(14, 16), S(20, 16), and T(22, 8)? Round to the nearest hundredth, if necessary.

Answer 1

check the picture below.

so... you can pretty much see how long RS and QT are, you can just count the units off the grid.

now, let's find QR's length




and let's also find the length for ST




so, add the lengths of all sides, and that's the perimeter of the trapezoid.

Answer 2

The Perimeter is 38.25 units.

Explanation:

The vertices of trapezoid are Q(8, 8), R(14, 16), S(20, 16), and T(22, 8). we have to find the perimeter of trapezoid.

Perimeter is sum of all sides of trapezoid i.e

Perimeter=QR+RS+ST+TQ

By distance formula,

`QR=√((16-8)^2+(14-8)^2)=√(64+36)=√(100)=10 units\\\\RS=√((20-14)^2+(16-16)^2)=√(6^2)=6units\\\\ST=√((22-20)^2+(8-16)^2)=√(4+64)=√(68)=8.25units\\\\TQ=√((8-22)^2+(8-8)^2)=√(14^2)=14units`

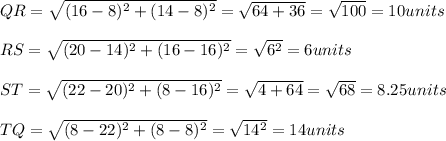
Perimeter=QR+RS+ST+TQ

=10+6+8.25+14=38.25 units.