Answer:
3 inches.
Explanation:
As the equation has a positive coefficient of
 , the graph is a parabola that open up. So, the minimun height value will be the y value of the vertex. Now, the vertex is
, the graph is a parabola that open up. So, the minimun height value will be the y value of the vertex. Now, the vertex is
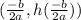
where b=-1 and a=0.01. Then,

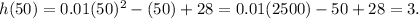
Then, the lowest part of the rope (50) is 3 inches close to the ground.