Let's approach this problem by considering simple cases. We will consider two kinds of absolute value inequalities, depending on whether the absolute value is less than or greater than a constant.
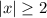
Let's consider this first case where the absolute value of x should be greater than or equal to 2. Intuition would tell us that if x is positive, it should be greater than or equal to 2 while if x is negative it should be less than or equal to -2. These two solutions cannot be combined together. This will be true for every expression with a greater than symbol favoring the absolute value. Answers for this case will just be written as
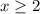
or

Now let's consider the following case:
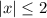
For this expression, our x needs to be less than or equal to 2 if it's positive and greater than or equal to -2 if it's negative. We'll notice that these two conditions actually intersect! It is possible to combine the answer into a
compound inequality. A compound inequality is an expression where two statements are joined by AND instead of OR (like what happened in the previous case). For this case we'll have the following answer:
 ANSWER:
ANSWER: Inequalities where 'greater than' symbols favor the CONSTANT will make use of compound inequalities.