Question

Identify the vertical asymptotes of f(x) = quantity x plus 6 over quantity x squared minus 9x plus 18

Answer 1

f(x) = x + 6 x + 6
------------------ = -----------------
x^2 - 9x + 18 (x - 6)(x - 3)

Vertical asymptotes occur when the denominator = zero

so here they are x = 6 and x = 3 (both of these makes the above denominator = zero)

Answer 2

`x=6\\x=3`

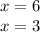
Explanation:

1)To identify its vertical asymptotes is to find them. To find them, we must consider the function on the denominator, then write this as an equation and find its zeros separately. Once found, there we have our vertical asymptotes.

So,

`f(x)=(x+6)/(x^(2)-9x+18)`

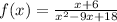
2) Finding the vertical asymptotes:

Firstly finding the roots via the roots via Sum and Product of this quadratic equation.

`x^(2)-9x+18=0\Rightarrow P(x)=(-6)*(-3)=18\\and\:\:S(x)=(-6)+(-3)\Rightarrow S=\left \{ 3,6 \right \}`

Rewriting:

`f(x)=(x+6)/((x+6)(x+3))`

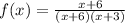
3) Graphing them below:

x=3 and x=6