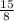Question

If sin Theta = 8/17 and Theta is in quadrant 2, then cot = _____. If necessary, use the slash mark ( / ) for a fraction bar.

Answer 1

sin theta= 8/17
cos theta= -15/17
tan theta= -8/15
cot theta= -15/8

Answer 2

In the question it is given Sin theta=
`(8)/(17)`

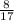
Sine theta is given to lie in second quadrant and the question is asking to find cot theta.

In second quadrant sine is positive while cot is negative.

Sine is the ratio of opposite and hypotenuse.

Sin theta =
`(opposite)/(hypotenuse)`

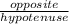
Cot theta=
`(Adjacent )/(opposite)`

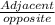
For the given question opposite is 8 and hypotenuse is 17.

We can find adjacent side by using Pythagoras Theorem

`c^(2) =a^(2) +b^(2)`

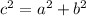
c is hypotenuse and a and b are the two legs

Substituting the value of c and b we have:

`17^(2) =8^(2) +b^(2)`

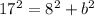
289=64+
`b^(2)`

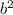
289-64=
`b^(2)`

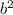
[ subtracting 64 both sides]

225=
`b^(2)`

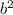
Taking root both sides

b=15

Cot theta=-
`(15)/(8)`