Question

Is the following statement always, never, or sometimes true?

A number raised to a negative exponent is negative.

always
never**
sometimes

Answer 1

The answer is sometimes

Answer 2

We need to complete the statement that " A number raised to a negative exponent is ___ negative"

Consider a number 'a' raised to a negative exponent say '-m'.

`a^(-m)`

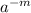
According to the law of exponents.

We get,
`a^(-m)=(1)/(a^(m))`

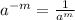
Now let us consider two cases:

Case 1 : If 'a' is a positive number, let a = 'x'.

Then,
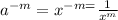`a^(-m)=x^(-m=)(1)/(x^(m))` which is positive.

Case 2: If 'a' is a negative number, let a= '-x '

Then,
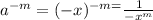`a^(-m)=(-x)^(-m=)(1)/(-x^(m))` which is negative.

Therefore, we can say that

" A number raised to a negative exponent is sometimes negative".