Question

What is the value of the 9th term in the following geometric sequence?

3, 12, 48, 192, ...

A. 96
B. 786,429
C. 105
D. 196,608

Answer 1

The correct option is (D) 196608.

Explanation:

The correct option is (D) 196608.

Answer 2

Answer: The correct option is (D) 196608.

Step-by-step explanation: We are given to find the value of the 9th term in the following geometric sequence :

3, 12, 48, 192, . . .

We know that

the n-th term of a geometric sequence with first term a and common ratio r is given by

`a_n=ar^(n-1).`

For the given sequence, we have

first term, a = 3 and the common ratio, r is given by

`r=(12)/(3)=(48)/(12)=(192)/(48)=~~.~~.~~.~~=4.`

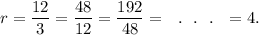
Therefore, the 9th term of the given sequence will be

`a_9=ar^(9-1)=3* 4^8=3*65536=196608.`

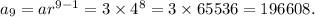
Thus, the required 9th term of the given sequence is 196608.

Option (D) is CORRECT.