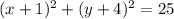Question

Write the standard equation of a circle that passes through (−4, 0) with center (−1, −4).

Answer 1

Modify the std eqn of a circle with center at (h,k) to find the radius r:

(-4+1)^2 + (0+4)^2 = r^2. Then 9 + 16 = 25, and so r^2 = 25, and r = +5.

The equation is (x+1)^2 + (y+4)^2 = 25.

Answer 2

the equation of a circle is defined by:
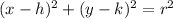
`(x - h)^(2) + (y - k)^(2) = r^(2)` where (h,k) is the center of the circle and "r" is the radius. So we need to find the radius, which is the distance between the center (-1,-4) and the point on the circle (-4, 0). Do this using the distance formula: d =
`\sqrt{( x_(2 -) x_(1))^2 + ( y_(2)- y_(1))^2 }`

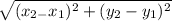
so distance =
`√((-4 - 0)^2 + (-1 + 4)^2) = √(25) = 5`
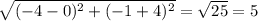
Now we just write the equation:
`(x +1)^2 + (y + 4)^2 = 25`