Question

Can you think of any 2x2 matrices d for which cd = dc for all 2x2 matrices c? give 2 different examples of such matricesd.

Answer 1

For any arbitrary 2x2 matrices
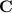
`\mathbf C` and
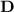
`\mathbf D`, only one choice of
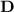
`\mathbf D` exists to satisfy
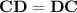
`\mathbf{CD}=\mathbf{DC}`, which is the identity matrix.

There is no other matrix that would work unless we place some more restrictions on
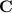
`\mathbf C`. One such restriction would be to ensure that
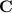
`\mathbf C` is not singular, or its determinant is non-zero. Then this matrix has an inverse, and taking
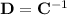
`\mathbf D=\mathbf C^(-1)` we'd get equality.