Question

An ellipse has an area of 4.71 in.2 and a minor axis that is 2.00 in. long. Solve for the major axis, and then sketch the ellipse using that dimension. Show only those dimensions needed for the area calculation. Note: Each grid unit = 0.25 inch.

Answer 1

Explanation:

The area of an ellipse can be calculated using:

`A=\pi *a*b`

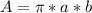
Where a is the radius of the major axis(half of the full length) and b is the radius of the minor axis(half of the full length. That means that in this case, the radius of the minor axis is half of 2, which is 1.

Substituting:

`A=\pi *a*1\\4.71=\pi *a\\(4.71)/(\pi ) =a\\a=1.5 inches\\`

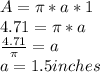
The length of the secondary axis is twice the size of the radius, which makes it 3.

Answer 2

by definition we have that the area of the ellipse is
A = pi * a * b
where
a: Semi-main axis
b: Semi-minor axis
Substituting and clearing:
a = A / (pi * b) = (4.71) / (PI * 1) = 1.50 in.
Therefore the main axis is
2 * a = 2 * (1.50) = 3in
Graphic attached.