Question

What is the recursive rule for this geometric sequence? 3, 3/2, 3/4, 3/8

Answer 1

I think that would be  an  = an-1 *  1/2    where an = nth term, and an-1 = previous term. 

Answer 2

`a_(n)=(a_(n-1))/(2)`

Explanation:

Let's look a the sequence:

`3, (3)/(2) ,(3)/(4) ,(3)/(8)`

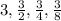
we can see that

`(3)/(2)=3*(1)/(2)`

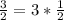
and

`(3)/(4) =(3)/(2)*(1)/(2)`

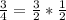
and

`(3)/(8)=(3)/(4) *(1)/(2)`

so each next number is equal to the previous number multiplied by
`(1)/(2)` or, in other other words, is the previous number divided by 2.

So the recursive formula must be:

`a_(n)=(a_(n-1))/(2)`

where
`a_(n)` is a number in the sequence, and
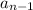`a_(n-1)` is the immediate previous number.