Question

The congruence theorem that can be used to prove △BAE ≅ △CAD is

A. SSS.
B. ASA.
C. SAS.
D. HL.

Answer 1

its D HL

Explanation:

Answer 2

Option is D.

The congruence theorem that can be used to prove △BAE ≅ △CAD is HL (Hypotenuse and leg of a right triangle.)

Explanation:

From the Figure:

Consider △BAE ≅ △CAD

∴
`\angle BAE=\angle DAC=90^(\circ)`

`BE=CD \left \{ Hypotenuse side\right \}`

`BA=AC \left \{One leg of the triangle are equal\right \}`

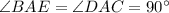
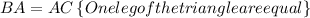
Therefore, by HL i.e, (Hypotenuse and leg of a right triangle) which implies that two right angle triangle are congruent if their hypotenuse and one corresponding leg of the triangle are equal.

Hence,
`\bigtriangleup BAE\simeq \bigtriangleup CAD` by HL congruence theorem.