The volume of a cube is increasing at a rate of 12 cm3/min. How fast is the surface area increasing when the length of an edge is 40 cm

Question

asked Jan 14, 2023 204k views

1 Answer

Nikesha · Answer 1 · 2023-01-20T07:29:40+0000

Answer:

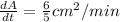
(dA)/(dt)=(6)/(5)cm^2/min

Explanation:

Given

(dV)/(dt)=12cm^3/min <-- The change in volume with respect to time

V=s^3 <-- Volume of a cube

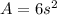A=6s^2 <-- Surface area of a cube

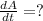(dA)/(dt)=? <-- The change in surface area with respect to time

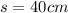s=40cm <-- Length of edge of cube

Solve for ds/dt:

V=s^3

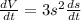
(dV)/(dt)=3s^2(ds)/(dt)

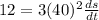
12=3(40)^2(ds)/(dt)

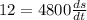
12=4800(ds)/(dt)

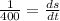
(1)/(400)=(ds)/(dt)

Solve for dA/dt:

A=6s^2

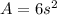
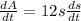
(dA)/(dt)=12s(ds)/(dt)

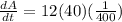
(dA)/(dt)=12(40)((1)/(400))

(dA)/(dt)=12((1)/(10))

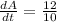
(dA)/(dt)=(12)/(10)

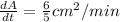
(dA)/(dt)=(6)/(5)cm^2/min

Therefore, the surface area of the cube is increasing at a rate of 6/5 cm²/min when the length of an edge is 40 cm.

Let me know if you need more help with related rates!