Question

Which statement best describes the domain and range of f(x) = –(7)^x and g(x) = 7^x?

f(x) and g(x) have the same domain and the same range.

f(x) and g(x) have the same domain but different ranges.

f(x) and g(x) have different domains but the same range.

f(x) and g(x) have different domains and different ranges.

Answer 1

B. f(x) and g(x) have same domain but different ranges.

Answer 2

f(x) and g(x) have the same domain but different ranges.

Explanation:

The domain of
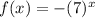`f(x)=-(7)^x` is:

`Domain: (-\infty, \infty)`

Because there is no any restriction. And its range is:

`Range: \{y\in R :y<0\}`

Because the minus sign is out of the parentheses, so no matter the value of x, the result will be always negative.

Now, The domain of
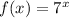`f(x)=7^x` is:

`Domain: (-\infty, \infty)`

As before, because there is no any restriction. And its range is:

`Range: \{y\in R :y>0\}`

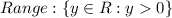
Because no matter the value of x this function is always positive since:

`a^(-x)=(1)/(a^x)`

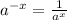
Therefore:

f(x) and g(x) have the same domain but different ranges.

I attached you the graphs.